技术干货 | 深入浅出谈人脸识别技术

在深度学习出现后,人脸识别技术才真正有了可用性。这是因为之前的机器学习技术中,难以从图片中取出合适的特征值。轮廓?颜色?眼睛?如此多的面孔,且随着年纪、光线、拍摄角度、气色、表情、化妆、佩饰挂件等等的不同,同一个人的面孔照片在照片象素层面上差别很大,凭借专家们的经验与试错难以取出准确率较高的特征值,自然也没法对这些特征值进一步分类。

深度学习的最大优势在于由训练算法自行调整参数权重,构造出一个准确率较高的f(x)函数,给定一张照片则可以获取到特征值,进而再归类。本文中笔者试图用通俗的语言探讨人脸识别技术,首先概述人脸识别技术,接着探讨深度学习有效的原因以及梯度下降为什么可以训练出合适的权重参数,最后描述基于CNN卷积神经网络的人脸识别。

一、人脸识别技术概述

人脸识别技术大致由人脸检测和人脸识别两个环节组成。

之所以要有人脸检测,不光是为了检测出照片上是否有人脸,更重要的是把照片中人脸无关的部分删掉,否则整张照片的像素都传给f(x)识别函数肯定就不可用了。人脸检测不一定会使用深度学习技术,因为这里的技术要求相对低一些,只需要知道有没有人脸以及人脸在照片中的大致位置即可。一般我们考虑使用OpenCV、dlib等开源库的人脸检测功能(基于专家经验的传统特征值方法计算量少从而速度更快),也可以使用基于深度学习实现的技术如MTCNN(在神经网络较深较宽时运算量大从而慢一些)。

在人脸检测环节中,我们主要关注检测率、漏检率、误检率三个指标,其中:

• 检测率:存在人脸并且被检测出的图像在所有存在人脸图像中的比例;
• 漏检率:存在人脸但是没有检测出的图像在所有存在人脸图像中的比例;
• 误检率:不存在人脸但是检测出存在人脸的图像在所有不存在人脸图像中的比例。

当然,检测速度也很重要。本文不对人脸检测做进一步描述。

在人脸识别环节,其应用场景一般分为1:1和1:N。

1:1就是判断两张照片是否为同一个人,通常应用在人证匹配上,例如身份证与实时抓拍照是否为同一个人,常见于各种营业厅以及后面介绍的1:N场景中的注册环节。而1:N应用场景,则是首先执行注册环节,给定N个输入包括人脸照片以及其ID标识,再执行识别环节,给定人脸照片作为输入,输出则是注册环节中的某个ID标识或者不在注册照片中。可见,从概率角度上来看,前者相对简单许多,且由于证件照通常与当下照片年代间隔时间不定,所以通常我们设定的相似度阈值都是比较低的,以此获得比较好的通过率,容忍稍高的误识别率。

而后者1:N,随着N的变大,误识别率会升高,识别时间也会增长,所以相似度阈值通常都设定得较高,通过率会下降。这里简单解释下上面的几个名词:误识别率就是照片其实是A的却识别为B的比率;通过率就是照片确实是A的,但可能每5张A的照片才能识别出4张是A其通过率就为80%;相似度阈值是因为对特征值进行分类是概率行为,除非输入的两张照片其实是同一个文件,否则任何两张照片之间都有一个相似度,设定好相似度阈值后唯有两张照片的相似度超过阈值,才认为是同一个人。所以,单纯的评价某个人脸识别算法的准确率没有意义,我们最需要弄清楚的是误识别率小于某个值时(例如0.1%)的通过率。不管1:1还是1:N,其底层技术是相同的,只是难度不同而已。

取出人脸特征值是最难的,那么深度学习是如何取特征值的?

假定我们给出的人脸照片是100*100像素大小,由于每个像素有RGB三个通道,每个像素通道由0-255范围的字节表示,则共有3个100*100的矩阵计3万个字节作为输入数据。深度学习实际上就是生成一个近似函数,把上面的输入值转化为可以用作特征分类的特征值。那么,特征值可以是一个数字吗?当然不行,一个数字(或者叫标量)是无法有效表示出特征的。通常我们用多个数值组成的向量表示特征值,向量的维度即其中的数值个数。特征向量的维度并非越大越好,Google的FaceNet项目(参见http://arxiv.org/abs/1503.03832论文)做过的测试结果显示,128个数值组成的特征向量结果最好,如下图所示:

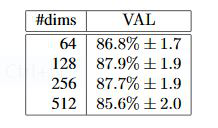
那么,现在问题就转化为怎么把3*100*100的矩阵转化为128维的向量,且这个向量能够准确的区分出不同的人脸?

假定照片为x,特征值为y,也就是说存在一个函数f(x)=y可以完美的找出照片的人脸特征值。现在我们有一个f*(x)近似函数,其中它有参数w(或者叫权重w)可以设置,例如写成f*(x;w),若有训练集x及其id标识y,设初始参数p1后,那么每次f*(x;w)得到的y`与实际标识y相比,若正确则通过,若错误则适当调整参数w,如果能够正确的调整好参数w,f*(x;w)就会与理想中的f(x)函数足够接近,我们就获得了概率上足够高准确率的f*(x;w)函数。这一过程叫做监督学习下的训练。而计算f*(x;w)值的过程因为是正常的函数运算,我们称为前向运算,而训练过程中比较y`与实际标识id值y结果后,调整参数p的过程则是反过来的,称为反向传播。

由于我们传递的x入参毕竟是一张照片,照片既有对焦、光线、角度等导致的不太容易衡量的质量问题,也有本身的像素数多少问题。如果x本身含有的数据太少,即图片非常不清晰,例如28*28像素的照片,那么谁也无法准确的分辨出是哪个人。可以想见,必然像素数越多识别也越准,但像素数越多导致的计算、传输、存储消耗也越大,我们需要有根据地找到合适的阈值。下图是FaceNet论文的结果,虽然只是一家之言,但Google的严谨态度使得数据也很有参考价值。

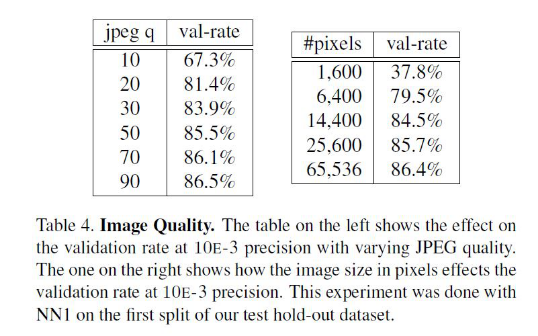
从图中可见,排除照片其他质量外,像素数至少也要有100*100(纯人脸部分)才能保证比较高的识别率。

二、深度学习技术的原理

由清晰的人脸照转化出的像素值矩阵,应当设计出什么样的函数f(x)转化为特征值呢?这个问题的答案依赖于分类问题。即,先不谈特征值,首先如何把照片集合按人正确地分类?这里就要先谈谈机器学习。机器学习认为可以从有限的训练集样本中把算法很好地泛化。所以,我们先找到有限的训练集,设计好初始函数f(x;w),并已经量化好了训练集中x->y。如果数据x是低维的、简单的,例如只有二维,那么分类很简单,如下图所示:

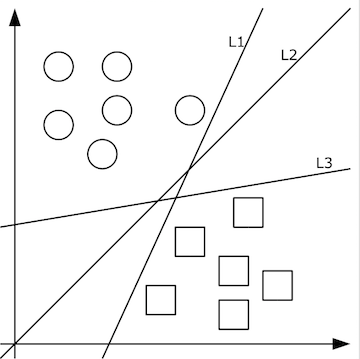
上图中的二维数据x只有方形和圆形两个类别y,很好分,我们需要学习的分类函数用最简单的f(x,y)=ax+by+c就能表示出分类直线。例如f(x,y)大于0时表示圆形,小于0时表示方形。

给定随机数作为a,c,b的初始值,我们通过训练数据不断的优化参数a,b,c,把不合适的L1、L3等分类函数逐渐训练成L2,这样的L2去面对泛化的测试数据就可能获得更好的效果。然而如果有多个类别,就需要多条分类直线才能分出,如下图所示:

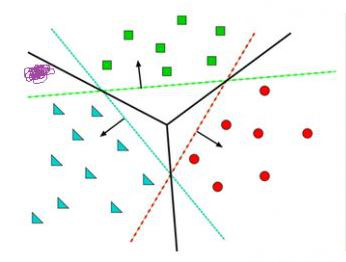
这其实相当于多条分类函数执行与&&、或||操作后的结果。这个时候还可能用f1>0 && f2<0 && f3>0这样的分类函数,但如果更复杂的话,例如本身的特征不明显也没有汇聚在一起,这种找特征的方式就玩不转了,如下图所示,不同的颜色表示不同的分类,此时的训练数据完全是非线性可分的状态:

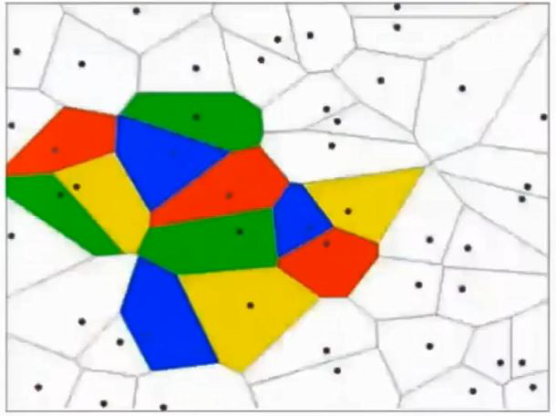
这个时候,我们可以通过多层函数嵌套的方法来解决,例如f(x)=f1(f2(x)),这样f2函数可以是数条直线,而f1函数可以通过不同的权重w以及激励函数完成与&&、或||等等操作。这里只有两层函数,如果函数嵌套层数越多,它越能表达出复杂的分类方法,这对高维数据很有帮助。例如我们的照片毫无疑问就是这样的输入。所谓激励函数就是把函数f计算出的非常大的值域转化为[0,1]这样较小的值域,这允许多层函数不断地前向运算、分类。

前向运算只是把输入交给f1(x,w1)函数,计算出的值再交给f2(y1,w2)函数,依次类推,很简单就可以得到最终的分类值。但是,因为初始的w权重其实没有多大意义,它得出的分类值f*(x)肯定是错的,在训练集上我们知道正确的值y,那么事实上我们其实是希望y-f*(x)的值最小,这样分类就越准。这其实变成了求最小值的问题。当然,y-f*(x)只是示意,事实上我们得到的f*(x)只是落到各个分类上的概率,把这个概率与真实的分类相比较得到最小值的过程,我们称为损失函数,其值为loss,我们的目标是把损失函数的值loss最小化。在人脸识别场景中,softmax是一个效果比较好的损失函数,我们简单看下它是如何使用的。

比如我们有训练数据集照片对应着cat、dog、ship三个类别,某个输入照片经过函数f(x)=x*W+b,前向运算得到该照片属于这3个分类的得分值。此时,这个函数被称为得分函数,如下图所示,假设左边关于猫的input image是一个4维向量[56,231,24,2],而W权重是一个4*3的矩阵,那么相乘后再加上向量[1.1,3.2,-1.2]可得到在cat、 dog、ship三个类别上的得分:

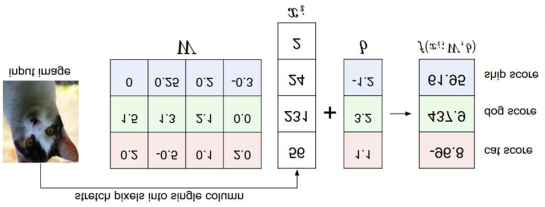
从上图示例可见,虽然输入照片是猫,但得分上属于狗的得分值437.9最高,但究竟比猫和船高多少呢?很难衡量!如果我们把得分值转化为0-100的百分比概率,这就方便度量了。这里我们可以使用sigmoid函数,如下图所示:

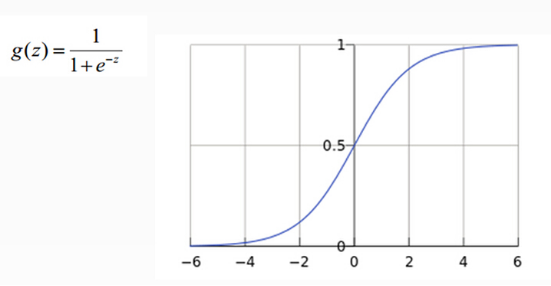
从上图公式及图形可知,sigmoid可以把任意实数转换为0-1之间的某个数作为概率。但sigmoid概率不具有归一性,也就是说我们需要保证输入照片在所有类别的概率之和为1,这样我们还需要对得分值按softmax方式做以下处理:

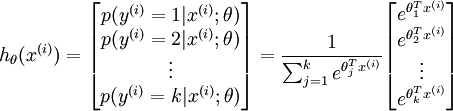
这样给定x后可以得到x在各个类别下的概率。假定三个类别的得分值分别为3、1、-3,则按照上面的公式运算后可得概率分别为[0.88、0.12、0],计算过程如下图所示:

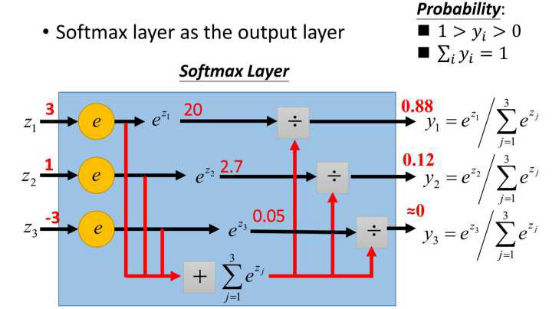
然而实际上x对应的概率其实是第一类,比如[1,0,0],现在拿到的概率(或者可称为似然)是[0.88、0.12、0]。那么它们之间究竟有多大的差距呢?这个差距就是损失值loss。如何获取到损失值呢?在softmax里我们用互熵损失函数计算量最小(方便求导),如下所示:

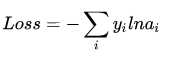
其中i就是正确的分类,例如上面的例子中其loss值就是-ln0.88。这样我们有了损失函数f(x)后,怎么调整x才能够使得函数的loss值最小呢?这涉及到微分导数。

三、梯度下降

梯度下降就是为了快速的调整权重w,使得损失函数f(x;w)的值最小。因为损失函数的值loss最小,就表示上面所说的在训练集上的得分结果与正确的分类值最接近!

导数求的是函数在某一点上的变化率。例如从A点开车到B点,通过距离和时间可以算出平均速度,但在其中C点的瞬时速度是多少呢?如果用x表示时间,f(x)表示车子从A点驶出的距离,那么在x0的瞬时速度可以转化为:从x0时再开一个很小的时间,例如1秒,那么这一秒的平均速度就是这一秒开出的距离除以1秒,即(f(1+x0)-f(x0))/1。如果我们用的不是1秒而是1微秒,那么这个1微秒内的平均速度必然更接近x0时的瞬时速度。于是,到该时间段t趋向于0时,我们就得到了x0时的瞬时速度。这个瞬时速度就是函数f在x0上的变化率,所有x上的变化率就构成了函数f(x)的导数,称为f`(x)。即:

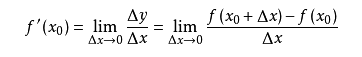
从几何意义上看,变化率就变成了斜率,这更容易理解怎样求函数的最小值。例如下图中有函数y=f(x)用粗体黑线表示,其在P0点的变化率就是切线红线的斜率:

可以形象的看出,当斜率的值为正数时,把x向左移动变小一些,f(x)的值就会小一些;当斜率的值为负数时,把x向右移动变大一些,f(x)的值也会小一些,如下图所示:

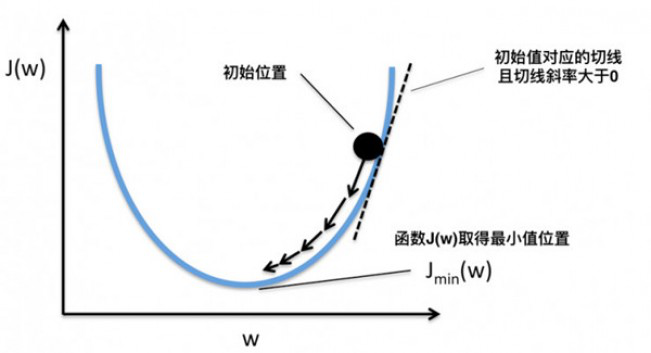
这样,斜率为0时我们其实就得到了函数f在该点可以得到最小值。那么,把x向左或者向右移一点,到底移多少呢?如果移多了,可能移过了,如果移得很少,则可能要移很久才能找到最小点。还有一个问题,如果f(x)操作函数有多个局部最小点、全局最小点时,如果x移的非常小,则可能导致通过导数只能找到某个并不足够小的局部最小点。如下图所示:

蓝色的为局部最小点,红色是全局最小点。所以x移动多少是个问题,x每次的移动步长过大或者过小都可能导致找不到全局最小点。这个步长除了跟导数斜率有关外,我们还需要有一个超参数来控制它的移动速度,这个超参数称为学习率,由于它很难优化,所以一般需要手动设置而不能自动调整。考虑到训练时间也是成本,我们通常在初始训练阶段把学习率设的大一些,越往后学习率设的越小。

那么每次移动的步长与导数的值有关吗?这是自然的,导数的正负值决定了移动的方向,而导数的绝对值大小则决定了斜率是否陡峭。越陡峭则移动的步长应当越大。所以,步长由学习率和导数共同决定。就像下面这个函数,λ是学习率,而∂F(ωj) / ∂ωj是在ωj点的导数。

ωj = ωj – λ ∂F(ωj) / ∂ωj

根据导数判断损失函数f在x0点上应当如何移动,才能使得f最快到达最小值的方法,我们称为梯度下降。梯度也就是导数,沿着负梯度的方向,按照梯度值控制移动步长,就能快速到达最小值。当然,实际上我们未必能找到最小点,特别是本身存在多个最小点时,但如果这个值本身也足够小,我们也是可以接受的,如下图所示:

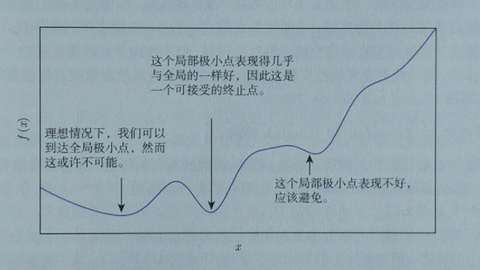
以上我们是以一维数据来看梯度下降,但我们的照片是多维数据,此时如何求导数?又如何梯度下降呢?此时我们需要用到偏导数的概念。其实它与导数很相似,因为x是多维向量,那么我们假定计算Xi的导数时,x上的其他数值不变,这就是Xi的偏导数。此时应用梯度下降法就如下图所示,θ是二维的,我们分别求θ0和θ1的导数,就可以同时从θ0和θ1两个方向移动相应的步长,寻找最低点,如下图所示:

前文说过,根据有限的训练集,去适应无限的测试集,当然训练集容量越大效果就越好。但是,训练集如果很大,那么每次都根据全部数据执行梯度下降计算量就太大了。此时,我们选择每次只取全部训练集中的一小部分(究竟多少,一般根据内存和计算量而定),执行梯度下降,不断的迭代,根据经验一样可以快速地把梯度降下来。这就是随机梯度下降。

上面的梯度下降法只能对f函数的w权重进行调整,而上文中我们说过实际是多层函数套在一起,例如f1(f2(x;w2);w1),那么怎么求对每一层函数输入的导数呢?这也是所谓的反向传播怎样继续反向传递下去呢?这就要提到链式法则。其实质为,本来y对x的求导,可以通过引入中间变量z来实现,如下图所示:

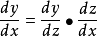
这样,y对x的导数等价于y对z的导数乘以z对x的偏导。当输入为多维时则有下面的公式:

如此,我们可以得到每一层函数的导数,这样可以得到每层函数的w权重应当调整的步长,优化权重参数。

由于函数的导数很多,例如resnet等网络已经达到100多层函数,所以为区别传统的机器学习,我们称其为深度学习。

深度学习只是受到神经科学的启发,所以称为神经网络,但实质上就是上面提到的多层函数前向运算得到分类值,训练时根据实际标签分类取损失函数最小化后,根据随机梯度下降法来优化各层函数的权重参数。人脸识别也是这么一个流程。以上我们初步过完多层函数的参数调整,但函数本身应当如何设计呢?

四、基于CNN卷积神经网络进行人脸识别

我们先从全连接网络谈起。Google的TensorFlow游乐场里可以直观的体验全连接神经网络的威力,这是游乐场的网址:http://playground.tensorflow.org/,浏览器里就可以做神经网络训练,且过程与结果可视化。如下图所示:

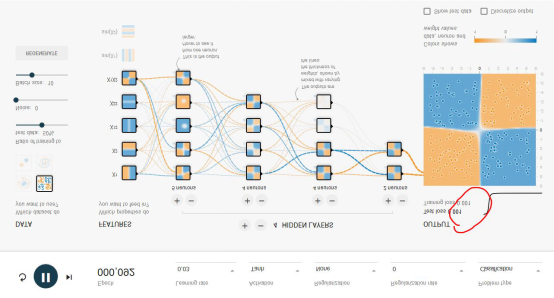
这个神经网络游乐场共有1000个训练点和1000个测试点,用于对4种不同图案划分出蓝色点与黄色点。DATA处可选择4种不同图案。

整个网络的输入层是FEATURES(待解决问题的特征),例如x1和x2表示垂直或者水平切分来划分蓝色与黄色点,这是最容易理解的2种划分点的方法。其余5种其实不太容易想到,这也是传统的专家系统才需要的,实际上,这个游乐场就是为了演示,1、好的神经网络只用最基本的x1,x2这样的输入层FEATURES就可以完美的实现;2、即使有很多种输入特征,我们其实并不清楚谁的权重最高,但好的神经网络会解决掉这个问题。

隐层(HIDDEN LAYERS)可以随意设置层数,每个隐层可以设置神经元数。实际上神经网络并不是在计算力足够的情况下,层数越多越好或者每层神经元越多越好。好的神经网络架构模型是很难找到的。本文后面我们会重点讲几个CNN经典网络模型。然而,在这个例子中,多一些隐层和神经元可以更好地划分。

epoch是训练的轮数。红色框出的loss值是衡量训练结果的最重要指标,如果loss值一直是在下降,比如可以低到0.01这样,就说明这个网络训练的结果好。loss也可能下降一会又突然上升,这就是不好的网络,大家可以尝试下。learning rate初始都会设得高些,训练到后面都会调低些。Activation是激励函数,目前CNN都在使用Relu函数。

了解了神经网络后,现在我们回到人脸识别中来。每一层神经元就是一个f函数,上面的四层网络就是f1(f2(f3(f4(x))))。然而,就像上文所说,照片的像素太多了,全连接网络中任意两层之间每两个神经元都需要有一次计算。特别之前提到的,复杂的分类依赖于许多层函数共同运算才能达到目的。当前的许多网络都是多达100层以上,如果每层都有3*100*100个神经元,可想而知计算量有多大!于是CNN卷积神经网络应运而生,它可以在大幅降低运算量的同时保留全连接网络的威力。

CNN认为可以只对整张图片的一个矩形窗口做全连接运算(可称为卷积核),滑动这个窗口以相同的权重参数w遍历整张图片后,可以得到下一层的输入,如下图所示:

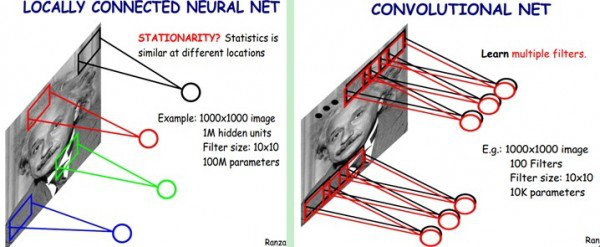
CNN中认为同一层中的权重参数可以共享,因为同一张图片的各个不同区域具有一定的相似性。这样原本的全连接计算量过大问题就解决了,如下图所示:

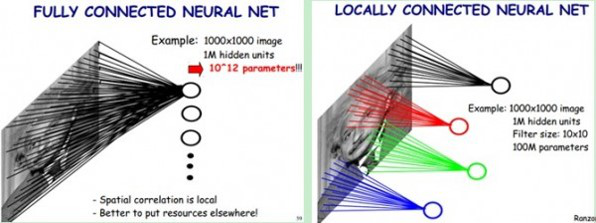
结合着之前的函数前向运算与矩阵,我们以一个动态图片直观的看一下前向运算过程:

这里卷积核大小与移动的步长stride、输出深度决定了下一层网络的大小。同时,核大小与stride步长在导致上一层矩阵不够大时,需要用padding来补0(如上图灰色的0)。以上就叫做卷积运算,这样的一层神经元称为卷积层。上图中W0和W1表示深度为2。

CNN卷积网络通常在每一层卷积层后加一个激励层,激励层就是一个函数,它把卷积层输出的数值以非线性的方式转换为另一个值,在保持大小关系的同时约束住值范围,使得整个网络能够训练下去。在人脸识别中,通常都使用Relu函数作为激励层,Relu函数就是max(0,x),如下所示:

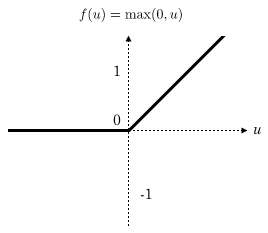
可见 Relu的计算量其实非常小!

CNN中还有一个池化层,当某一层输出的数据量过大时,通过池化层可以对数据降维,在保持住特征的情况下减少数据量,例如下面的4*4矩阵通过取最大值降维到2*2矩阵:

上图中通过对每个颜色块筛选出最大数字进行池化,以减小计算数据量。

通常网络的最后一层为全连接层,这样一般的CNN网络结构如下所示:

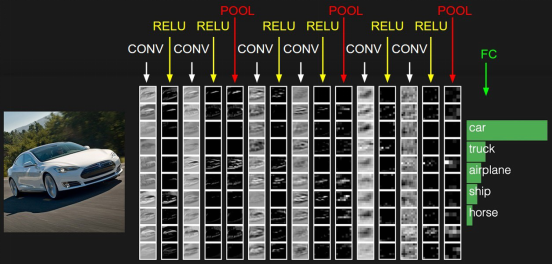
CONV就是卷积层,每个CONV后会携带RELU层。这只是一个示意图,实际的网络要复杂许多。目前开源的Google FaceNet是采用resnet v1网络进行人脸识别的,关于resnet网络请参考论文http://arxiv.org/abs/1602.07261,其完整的网络较为复杂,这里不再列出,也可以查看基于TensorFlow实现的Python代码http://github.com/davidsandberg/facenet/blob/master/src/models/inception_resnet_v1.py,注意slim.conv2d含有Relu激励层。

以上只是通用的CNN网络,由于人脸识别应用中不是直接分类,而是有一个注册阶段,需要把照片的特征值取出来。如果直接拿softmax分类前的数据作为特征值效果很不好,例如下图是直接将全连接层的输出转化为二维向量,在二维平面上通过颜色表示分类的可视化表示:

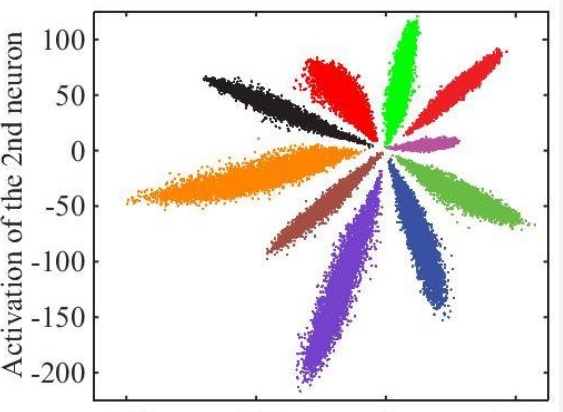
可见效果并不好,中间的样本距离太近了。通过centor loss方法处理后,可以把特征值间的距离扩大,如下图所示:

这样取出的特征值效果就会好很多。

实际训练resnet v1网络时,首先需要关注训练集照片的质量,且要把不同尺寸的人脸照片resize到resnet1网络首层接收的尺寸大小。另外除了上面提到的学习率和随机梯度下降中每一批batchsize图片的数量外,还需要正确的设置epochsize,因为每一轮epoch应当完整的遍历完训练集,而batchsize受限于硬件条件一般不变,但训练集可能一直在变大,这样应保持epochsize*batchsize接近全部训练集。训练过程中需要密切关注loss值是否在收敛,可适当调节学习率。

最后说一句,目前人脸识别效果的评价唯一通行的标准是LFW(即Labeled Faces in the Wild,参见http://vis-www.cs.umass.edu/lfw/),它包含大约6000个不同的人的12000张照片,许多算法都依据它来评价准确率。但它有两个问题,一是数据集不够大,二是数据集场景往往与真实应用场景并不匹配。所以如果某个算法称其在LFW上的准确率达到多么的高,并不能反应其真实可用性。

作者介绍:陶辉,杭州智链达数据有限公司技术总监&联合创始人,《深入理解Nginx:模块开发与架构解析》作者。

来源：程序师